Introduction of AFIR
The AFIR method induces various structural deformations by pushing fragments A and B together or by pulling them apart. The artificial force is applied to the target system by the following AFIR function,
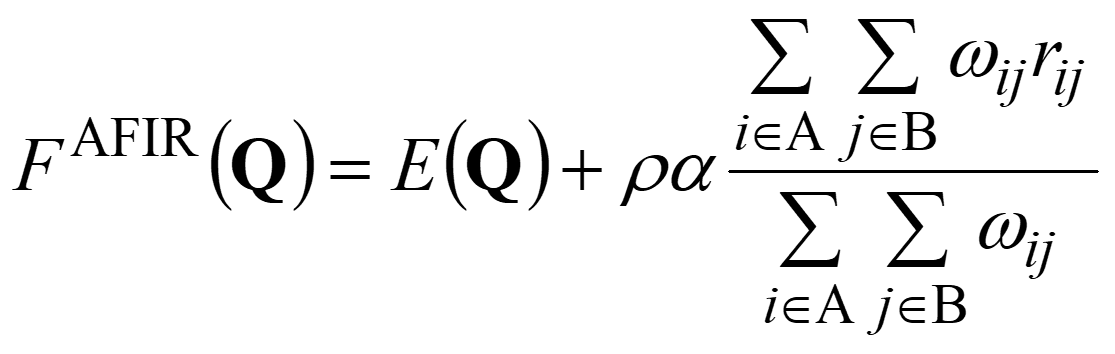
where E(Q) is the PES of geometrical parameters Q and the second term applies the artificial force to the system. The constant parameter α defines the strength of the force, and ρ is set to either 1.0 or −1.0. The second term is given as a weighted sum of the interatomic distance rij between atoms i and j, and the weight ωij is defined as,
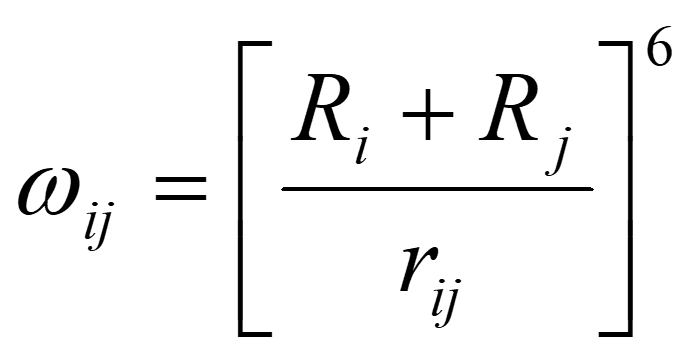
where Ri and Rj are the covalent radii of atoms i and j, respectively. The force parameter α is obtained as,
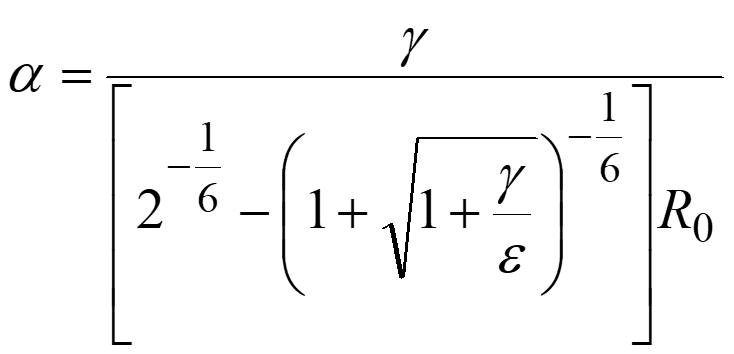
where R0 and ε are parameters of the Lennard-Jones potential for Ar—Ar interaction and set to the standard value, i.e., 3.8164 Å and 1.0061 kJ/mol, respectively. The α corresponds to the mean force that an Ar—Ar pair feels while it moves from the minimum point to the turning point in their direct collision with collision energy γ. The model collision energy parameter γ, which provides an approximate upper limit of the barrier height that the system can overcome by the AFIR method, is defined by the user. In application to thermal reactions, the value of γ is often decided using the following equation,
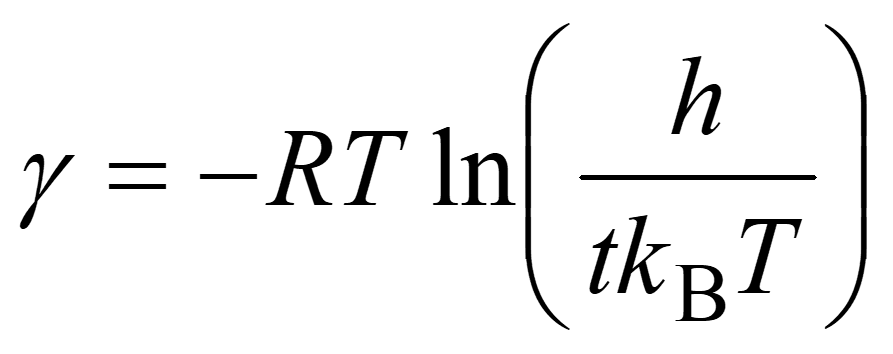
where R, T, h, t, and kB are the gas constant, temperature, the Plank constant, reaction time, and the Boltzmann constant, respectively. Values of T and t depend on reaction conditions. To allow for paths having somewhat high barriers, t should be set to a larger value than the actual reaction time tactual, e.g., t = 10 tactual.
The path through which the system passes during the minimization of the AFIR function is called AFIR path. The AFIR path changes depending on the following two conditions: the initial structure and the fragment pair A and B. In the MC-AFIR algorithm, different AFIR paths are obtained by calculating them starting from different initial structures. On the other hand, the SC-AFIR algorithm finds different AFIR paths by calculating them for different fragment pairs. More details of these two algorithms are described in the corresponding sections. Approximate EQs and TSs for E(Q) can be obtained as local minima and maxima, respectively, along the AFIR path. To improve the accuracy, relaxation of the AFIR path may be made before optimization of TSs. The locally updated planes (LUP) method is implemented. Approximate EQs and TSs either on the AFIR path or on the LUP path are optimized to actual EQs and TSs. Finally, IRC calculations are made starting from all obtained TSs. As long as an option which disables calculation of exact Hessian is not applied, normal mode analysis is done at all obtained EQs and TSs.
In the MC-AFIR algorithm, AFIR paths are sampled starting from various initial structures, where the fragments A and B are fixed to given ones throughout. The set of initial structures are generated automatically by giving mutual orientations and positions of two or more inputted molecules randomly. Optionally, the structure of each molecule can be read from a EQ-list prepared separately, where one of structures in the EQ-list is chosen randomly from the EQ-list and used as the corresponding part of the initial structure. In addition, there is an option with which initial structures are read from a structure list prepared by the user. After the calculation, a set of AFIR paths are obtained. Obtained AFIR paths need to be examined further; this can be done by the RePATH calculation which automatically applies LUP path optimization, EQ optimization, TS optimization, and IRC calculation, to all paths (either AFIR path, LUP path, or IRC path) that are read from previous results.
In the SC-AFIR algorithm, AFIR paths are calculated starting from EQs. The EQ is not necessarily a single molecule, but also H-bond clusters, metal clusters, van der Waals complexes, organometallic complexes, and so forth. From a single EQ, many different AFIR paths for different fragment pairs are searched. At each EQ structure, fragment pairs are defined systematically by a simple algorithm. All the procedures, i.e., AFIR path calculation, LUP path optimization, EQ optimization, TS optimization, and IRC calculation, are applied automatically in default. After completion of the calculation, one can draw the IRC path network using data in EQ-list and TS-list. Each path can be distinguished by three numbers i, j, and ρ; a path from EQi obtained by applying the artificial force to the j-th fragment pair with positive or negative (ρ = 1 or −1) sign of the AFIR function. During the search, the next path to be calculated is chosen by a simple stochastic algorithm, where the same path is not calculated twice or more. In this algorithm, the following parameter μi is computed for all EQs in the EQ-list.
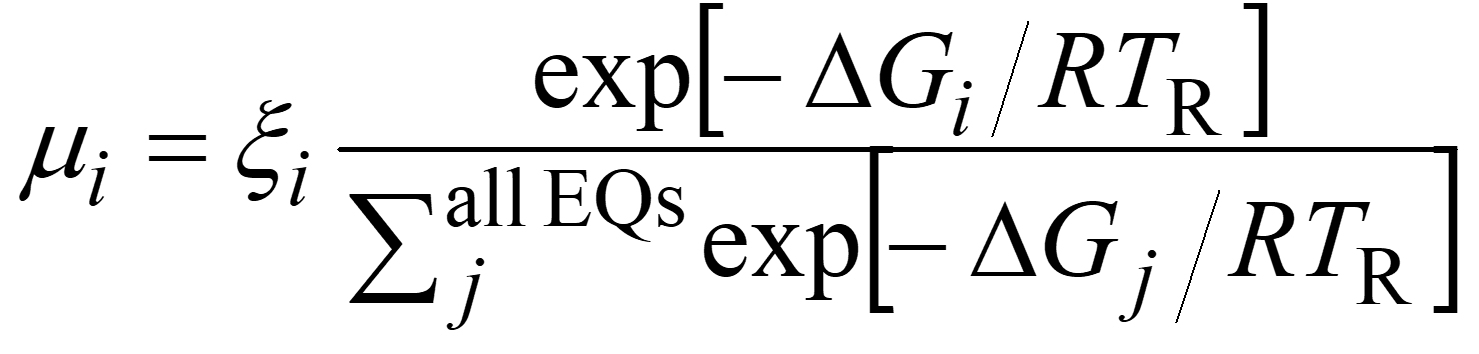
Then, an EQ which has the maximum value is chosen. In this equation, ξi is a random number between 0 and 1 and ΔGi is Gibbs free energy of EQi. The TR is a model temperature parameter, which determines how frequently high energy EQs are chosen, is usually set to a much higher value than the corresponding experimental temperature (in default, TR = 2981.5 K). Then, the combination of j and ρ is selected randomly. This path selection scheme controls the order of finding of EQs and TSs. It preferentially executes the search in low energy region, and EQs and TSs in such regions therefore tend to be found earlier than those in high energy regions. On the other hand, it does not affect the final results when all paths are computed.
For further details, see S. Maeda, et al., J. Comput. Chem., 2018, 39, 233–251. (this paper is Open Access).