Crossing point (MESX and MECI) optimization

MESX is a local minimum on the crossing seam between two adiabatic PESs of different spin or space symmetry. MECI is a local minimum on the conical intersection between two adiabatic PESs of the same spin and space symmetry. For their optimization, two algorithms are implemented in the GRRM17 program. In default, a penalty function method is used. The penalty function used is given below.

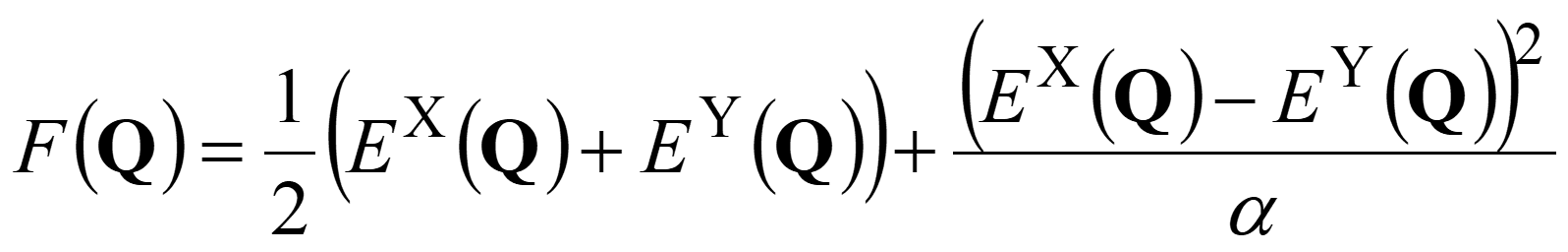
In this equation, E^X and E^Y are the adiabatic PESs of the two target states, Q is the coordinates, and α is a factor which is gradually decreased (in default starting from 30 kJ/mol) until the energy gap becomes smaller than a threshold (in default 1 kJ/mol). An example of input for an S₀/T₁ MESX optimization is:

# MIN/UB3LYP/6-31+G**
 
0 1
C          0.000000000000         -0.000000000000         -0.530465924142
O         -0.000000000000          0.000000000000          0.685412425504
H          0.000000000000          0.942437931730         -1.129067750681
H         -0.000000000000         -0.942437931730         -1.129067750681
Options
OptX
Second Input
UB3LYP/6-31+G**
0 3
END
MaxStepSize = 0.1
Stable=Opt
 

The OptX option is used together with the Second Input … END option. Lines between Second Input and END specify the computation method (UB3LYP/6-31+G**), charge (0) and spin multiplicity (3) of the second state (T₁). Use of MaxStepSize=x (x ≤ 0.1) and Stable=Opt options is recommended. When the MO GUESS option is used, two MO files, i.e., mmm.chk and mmm.chk_1, are required for the first and second states, respectively.

The gradient projection (GP) method is also available in the GRRM17 program for the more efficient and accurate optimization of MESX and MECI. In general, use of the GP method rather than the penalty function method is recommended. The GP method uses a composed gradient gGP,

where v^DGV corresponds to the difference gradient vector between the two PESs. The matrix P is so called projection matrix, and P for MESX optimization is defined as follows.

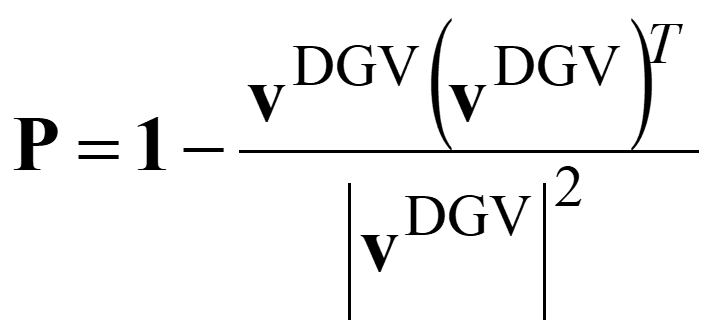
On the other hand, P for MECI optimization is defined as,

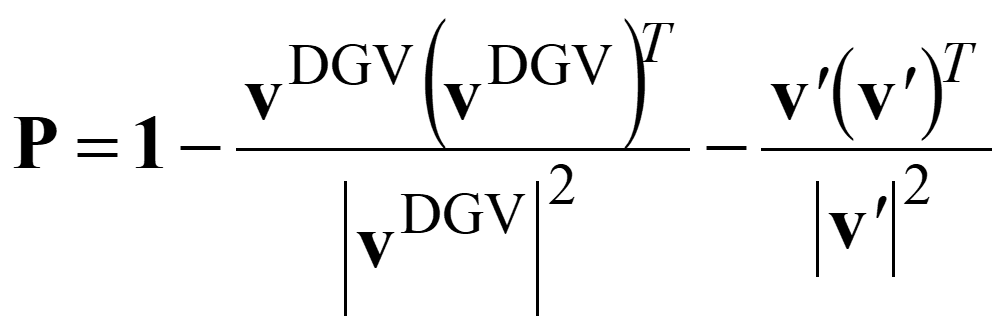
where v′ is an arbitrary vector not parallel to v^DGV on the branching plane (BP), and the derivative coupling vector or a vector obtained by the BP updating (BPU) method is used. In GRRM17, v′ is obtained by BPU as a unit vector perpendicular to v^DGV.

In the GP method, the user must specify which of MESX or MECI is optimized as OptX(Seam) or OptX(Conical). An example of input for an S₁/T₁ MESX optimization by the GP method is:

# MIN/B3LYP/6-31G*
 
0 3
C        -0.134291492000        -0.196773345000        -1.124500482000
C        -0.134291492000         1.001573655000        -0.412056482000
C        -0.134291492000         0.945472655000         0.982739518000
N        -0.134291491000        -0.196773345000         1.681769518000
C        -0.134291492000        -1.339019345000         0.982739518000
C        -0.134291492000        -1.395120345000        -0.412056482000
H        -0.134291492000        -0.196773345000        -2.210742482000
H        -0.134291492000         1.960231655000        -0.921273482000
H        -0.134291492000         1.863570655000         1.567903518000
H        -0.134291492000        -2.257117345000         1.567903518000
H        -0.134291492000        -2.353778345000        -0.921273482000
Options
OptX(Seam)
Second Input
B3LYP/6-31G* TD(Singlets,Root=1)
0 1
END
 

An example of input for an S₁/S₂ MECI optimization by the GP method is:

# MIN/B3LYP/6-31G* TD(Singlets,Root=2)
 
0 1
C        -0.134291492000        -0.196773345000        -1.124500482000
C        -0.134291492000         1.001573655000        -0.412056482000
C        -0.134291492000         0.945472655000         0.982739518000
N        -0.134291491000        -0.196773345000         1.681769518000
C        -0.134291492000        -1.339019345000         0.982739518000
C        -0.134291492000        -1.395120345000        -0.412056482000
H        -0.134291492000        -0.196773345000        -2.210742482000
H        -0.134291492000         1.960231655000        -0.921273482000
H        -0.134291492000         1.863570655000         1.567903518000
H        -0.134291492000        -2.257117345000         1.567903518000
H        -0.134291492000        -2.353778345000        -0.921273482000
Options
OptX(Conical)
Second Input
B3LYP/6-31G* TD(Singlets,Root=1)
0 1
END
 

In all the above three cases, the optimized structure is shown at the bottom of .log file. An example for the last case is given below:

Optimized structure, SYMMETRY = C2v
C         -0.134303084616         -0.196748741661         -1.118993676248
C         -0.134269246078          1.031134477157         -0.422304476327
C         -0.134348990720          1.018286946835          0.994546032469
N         -0.134238449684         -0.196839239816          1.542968592308
C         -0.134222120253         -1.411884026616          0.994597838790
C         -0.134256788065         -1.424523127868         -0.422215508425
H         -0.134415299558         -0.196570190604         -2.204392634880
H         -0.134233739061          1.991672107215         -0.924503045137
H         -0.134390300508          1.892090938864          1.632797538171
H         -0.134313301611         -2.285829756460          1.632686788269
H         -0.134215090842         -2.385296182045         -0.924034751064
ENERGY    = -248.116345824356 (-248.116345813233 : -248.116345835479)

The energy value corresponds to either the value of F(Q) or the mean energy of the two states, respectively, in the optimization result by the penalty function method or that by the GP method. The first value in the parenthesis corresponds to the energy of the state X, and the second value in the parenthesis is the energy of the state Y.

Availability

• FREQ
• MIN
• SADDLE
• IRC
• MC-AFIR
• SC-AFIR
• ReStruct

Available external software

• Gaussian 03/09/16
• Molpro
• GAMESS

Additional options frequently used with this option

• ShiftE